今天来记录一下前缀和的算法题
题目:

思路:
这道题题目中已经提到了前缀,提示已经很明显了,所以肯定是用前缀和的思想。
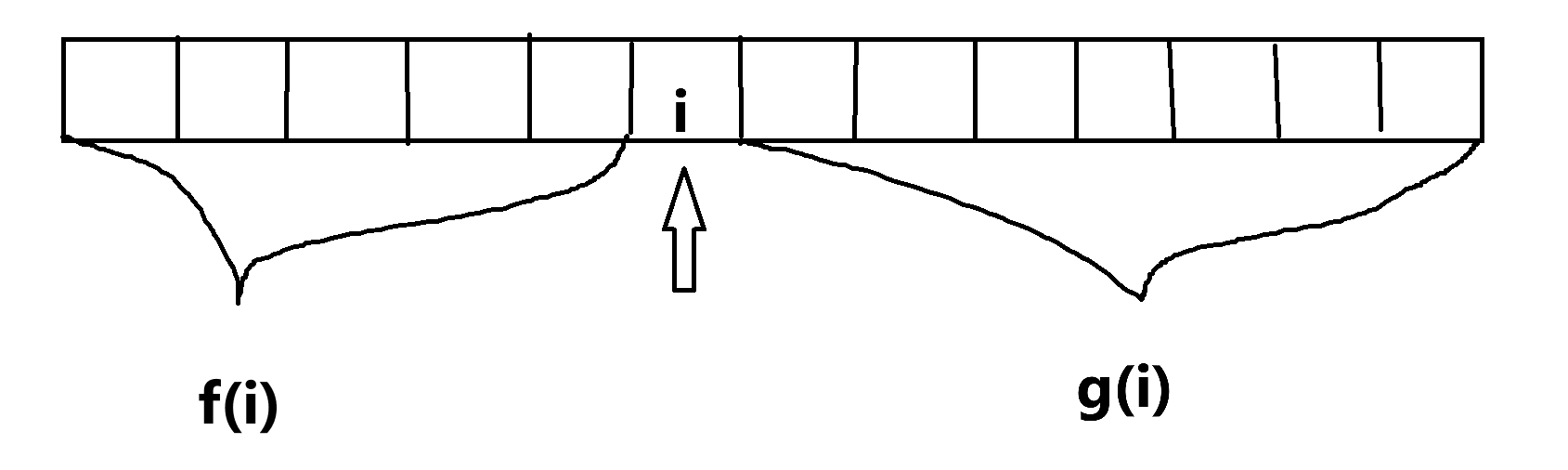
如图所示,nums[i]=f[i]*g[i],我们将f[i]和g[i]表示出来这段题就可以完成。
f[i]可以表示为 f[i]=f[i-1]*nums[i-1];
g[i]可以表示为g[i]=g[i+1]*nums[i+1];
这里我们会看到两个问题:
- f[i]的i必须要大于等于1,g[i]的i必须要小于等于length-1。
- f[0]和g[length-1]必须要单独处理,所以让f[0]=g[nums.length-1]=1;
最后重新定义一个结果数组记录并返回。
时空复杂度分析:
时间复杂度:O(n)
通过三个独立的 for 循环,每个循环遍历数组一次,因此总的时间复杂度为 O(n),其中 n 是数组的长度。
空间复杂度:O(n)
代码使用了三个辅助数组 f、g 和 res,每个数组的长度为 n,因此总的空间复杂度为 O(n)。
代码实现:
class Solution {
public int[] productExceptSelf(int[] nums) {
int f[]=new int [nums.length];
int g[]=new int [nums.length];
f[0]=g[nums.length-1]=1;
for(int i=1;i<nums.length;i++){
f[i]=f[i-1]*nums[i-1];
}
for(int i=nums.length-2;i>=0;i--){
g[i]=g[i+1]*nums[i+1];
}
int res[]=new int [nums.length];
for(int i=0;i<nums.length;i++){
res[i]=f[i]*g[i];
}
return res;
}
}总结:
本题为记录的第一个前缀和的算法,思路不难,后面会慢慢提高难度。